正如我们在前面的文章中所看到的,为了简化电路,我们使用电阻的串联和并联组合来降低电路的复杂性。此外,我们还经常使用电源转换方法来分析电路。然而,这些技术并不适用于所有类型的网络。
许多电路包含三端网络,例如星形(Y)或T型(T)网络以及三角形(Δ)或π型网络。这些网络可能是大型网络的一部分,也可能单独出现。这些网络的应用领域包括三相网络、匹配网络和电气滤波器等。这些网络通过另一种有用的技术——星三角变换——进行简化。
星形和三角形网络
在星形连接中,元件的连接方式是所有电阻或元件的一端都连接到一个公共点。由于三个电阻的排列方式类似于字母“Y”,因此这种星形网络也被称为Wye或Y网络。这种星形连接的等效电路可以重新绘制为T型网络(如图所示的四端网络)。大多数电气电路都包含这种T型网络。
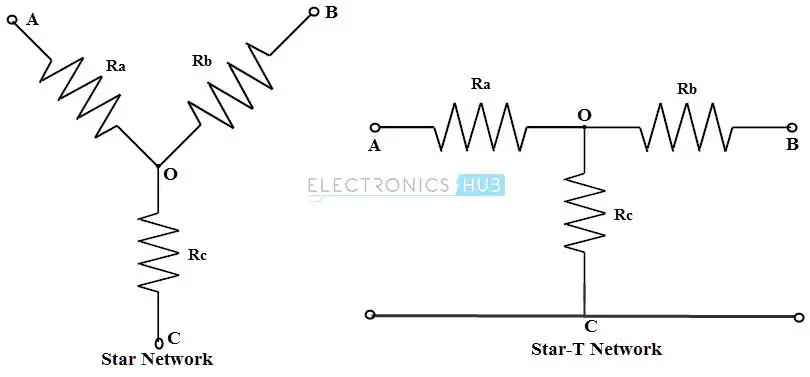
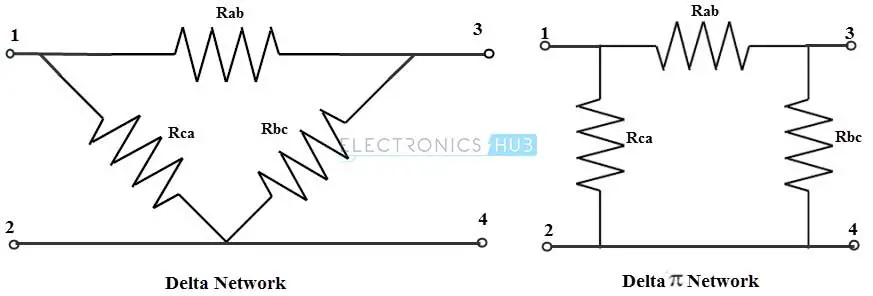
在三角形连接中,每个元件或线圈的端点连接到另一个元件或线圈的起点。这是三个元件的串联连接,形成一个三角形。名称表明,这种连接看起来像字母“Δ”。等效的三角形网络可以重新绘制为π型网络(如图所示的四端网络)。因此,这种网络也可以称为π型网络。
三角形到星形转换
当相似的端子对具有相同的阻抗时,可以实现星三角或三角星的转换。这种转换通过消除节点来产生等效网络。
让我们讨论三角形到星形的转换。假设 Rab、Rbc 和 Rca 是三角形网络中的三个串联电阻,而 Ra、Rb 和 Rc 是星形网络中的三个电阻。
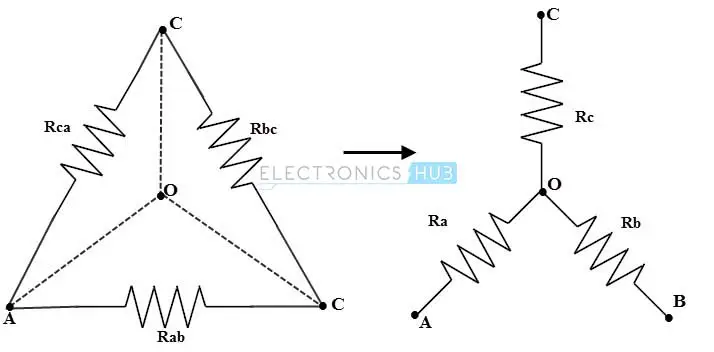
经过转换后,等效的星形网络和三角形网络在相似端子对之间测量时将具有相同的电阻。
考虑上图,端子 a 和 c 之间的等效电阻为
Ra+Rc=Rca∥(Rab+Rbc)
Ra+Rc=Rab+Rbc+RcaRca⋅(Rab+Rbc)(1)
端子 c 和 b 之间的等效电阻为
Rb+Rc=Rbc∥(Rab+Rca)
Rb+Rc=Rab+Rbc+RcaRbc⋅(Rab+Rca)(2)
端子 b 和 a 之间的等效电阻为
Rb+Ra=Rab∥(Rca+Rbc)
Rb+Ra=Rab+Rbc+RcaRab⋅(Rca+Rbc)(3)
将上述方程 (1)、(2) 和 (3) 结合,我们得到
Ra+Rb+Rc=Rab+Rbc+RcaRabRbc+RbcRca+RcaRab(4)
从方程 (4) 中减去方程 (2),我们得到
Ra=Rab+Rbc+RcaRabRca
从方程 (4) 中减去方程 (1),我们得到
Rb=Rab+Rbc+RcaRabRbc
从方程 (4) 中减去方程 (3),我们得到
Rc=Rab+Rbc+RcaRbcRca
这些 Ra、Rb 和 Rc 是从三角形等效电路转换过来的星形网络中的三个电阻值。
Ra=Rab+Rbc+RcaRabRca
Rb=Rab+Rbc+RcaRabRbc
Rc=Rab+Rbc+RcaRbcRca
从上述三个方程可以看出,对于给定的端子,星形网络中的等效电阻等于连接到同一端子的两个电阻(在三角形中)的乘积除以三角形网络中总电阻的和。
示例:
考虑下图,将三角形转换为星形或Wye电路,其中电阻值 R1=20 欧姆,R2=30 欧姆,R3=50 欧姆。

对于三角形到星形转换,等效电阻方程(针对此问题)为:
Ra=R1+R2+R3R1R2
Rb=R1+R2+R3R2R3
Rc=R1+R2+R3R1R3
因�此,总电阻 Rt=R1+R2+R3
=20+30+50
=100欧姆
Ra=R1+R2+R3R1R2=10020×30=6欧姆
类似地,
Rb=R1+R2+R3R2R3=10030×50=15欧姆
Rc=R1+R2+R3R1R3=10050×20=10欧姆
星形到三角形转换
使用相同的电阻表示方法,星形网络中的电阻为 Ra、Rb 和 Rc,三角形网络中的电阻为 Rab、Rbc 和 Rca。考虑下图所示的星形网络,其中通过电阻 Ra 的电流为
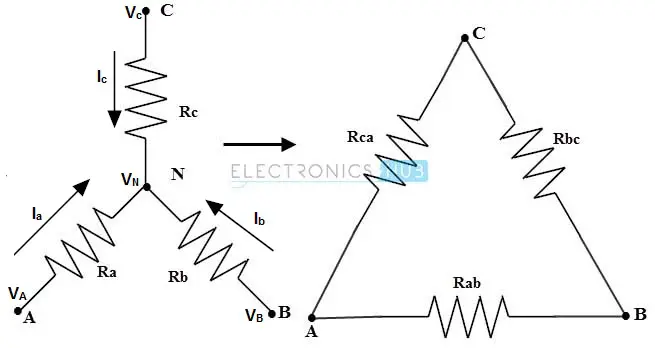 Ia=RaVa−Vn(1)
Ia=RaVa−Vn(1)
在星形网络的节点 N 应用基尔霍夫电流定律(KCL),我们得到
RaVa−Vn+RbVb−Vn+RcVc−Vn
Vn(Ra1+Rb1+Rc1)=RaVa+RbVb+RcVc
Vn=Ra1+Rb1+Rc1RaVa+RbVb+RcVc(2)
在三角形网络中,点 A 的电流为
Ia=RabVab+RacVac(3)
从方程 (1) 和 (3) 可得:
RaVa−Vn=RabVab+RacVac(4)
将方程 (2) 中的 Vn 值代入方程 (4),并经过简化后得到:
Rab=Ra+Rb+RcRaRb
Rac=Ra+Rc+RbRaRc
同样地,在星形网络中,电流 Ib 为:
Ib=RbVb−Vn(5)
在三角形网络中,电流 Ib 为:
Ib=RbcVbc+RbaVba(6)
将方程 (5) 和 (6) 等量齐观:
RbVb−Vn=RbcVbc+RbaVba(7)
将方程 (2) 代入方程 (7),并经过简化后得到:
Rbc=Rb+Rc+RaRbRc
因此,将三角形网络转换为等效星形或Wye网络所需的方程为:
Rab=Ra+Rb+RcRaRb=RcRaRb+RbRc+RcRa
Rbc=Rb+Rc+RaRbRc=RaRaRb+RbRc+RcRa
Rac=Ra+Rc+RbRaRc=RbRaRb+RbRc+RcRa
从上述三个方程可以看出,在给定的两个端子之间,等效的三角形电阻等于连接到这两个端子的两个电阻(在星形中)的和,再加上这两个电阻的乘积除以剩余的或第三个星形电阻。
示例:
考虑下图,将星形或Wye转换为三角形电路,其中星形网络中的电阻值分别为 R1=10 欧姆,R2=5 欧姆和 R3=20 欧姆。
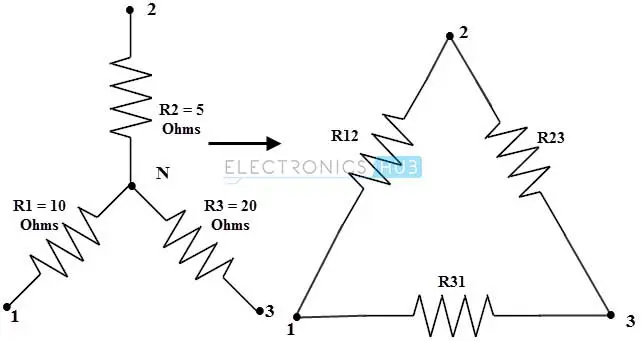
对于星形到三角形的转换,等效电阻方程(针对此问题)为:
R12=R1+R2+R3R1R2
R23=R2+R3+R1R2R3
R31=R1+R3+R2R1R3
通过简化上述方程,我们得到公共分子项为:
R1R2+R2R3+R1R3=10×5+10×20+20×5=350欧姆
因此:
R12=R3350=20350=17.5欧姆
R23=R1350=10350=35欧姆
R31=R2350=5350=70欧姆



